
Cuando vas por la calle mirando al suelo -sí, todos lo hacemos-, seguro te encuentras con varias tapas que llevan escrito el nombre de alguna compañía a cargo de los alcantarillados. Bien, pues todas tienen algo en común: son redondas. ¿Por qué? es una
pregunta que, seguramente, muchas personas en el mundo se hacen… ¿por qué no cuadradas o rectangulares? Como todo en la vida tiene un motivo, a continuación te explicamos la razón. Aunque esperamos que le hayas puesto atención a tu profesor
de geometría, porque se trata de razones matemáticas. De todas formas, seguro aprenderás un poco más. Y por cierto, la respuesta no es “porque el hoyo es redondo”.

De acuerdo al medio digital El País, la principal razón matemática es que la tapa no caiga por el agujero. Se trata de un tema de anchura: la distancia que hay entre dos puntos opuestos de una figura plana. Lo que en un círculo es completamente constante, puesto que la lejanía que hay entre cualquier parte del borde y su opuesto es el diámetro.
Lo anterior produce que sea prácticamente imposible que la tapa caiga por el agujero, de ninguna forma. Volvamos al comienzo de la nota. ¿Por qué no cuadradas ni rectangulares? Sencillo. Porque la anchura de estas figuras no es constante, es decir, la distancia entre dos vértices opuestos es mayor que cualquiera de los lados, por lo que existe el riesgo que las tapas, estando horizontales al suelo, caigan a la alcantarilla. No vamos a negar que existen tapas cuadradas y rectangulares, pero para esto también hay una justificación, aunque algo más simple: la profundidad de los hoyos es menor, por lo que si caen, se pueden volver a poner con facilidad.

Pero el círculo no es la única figura geométrica que tiene las propiedades necesarias para ser tapa de alcantarilla. De hecho, cualquier polígono regular con un número impar de lados puede serlo. ¿Cómo? Convirtiéndolos en polígonos de Reuleaux, creados por el ingeniero alemán Franz Reuleaux en el siglo XIX aunque, según cuenta la historia, aparecía ya en algunos escritos de Leonardo Da Vinci. Pongámonos friki: el triángulo de Reuleaux es el más fácil de construir desde la base de uno equilátero, trazando tres circunferencias cuyos centros sean los vértices de la figura. ¿Todo bien? Pues, lo que queda al medio de la imagen es lo que queríamos lograr.
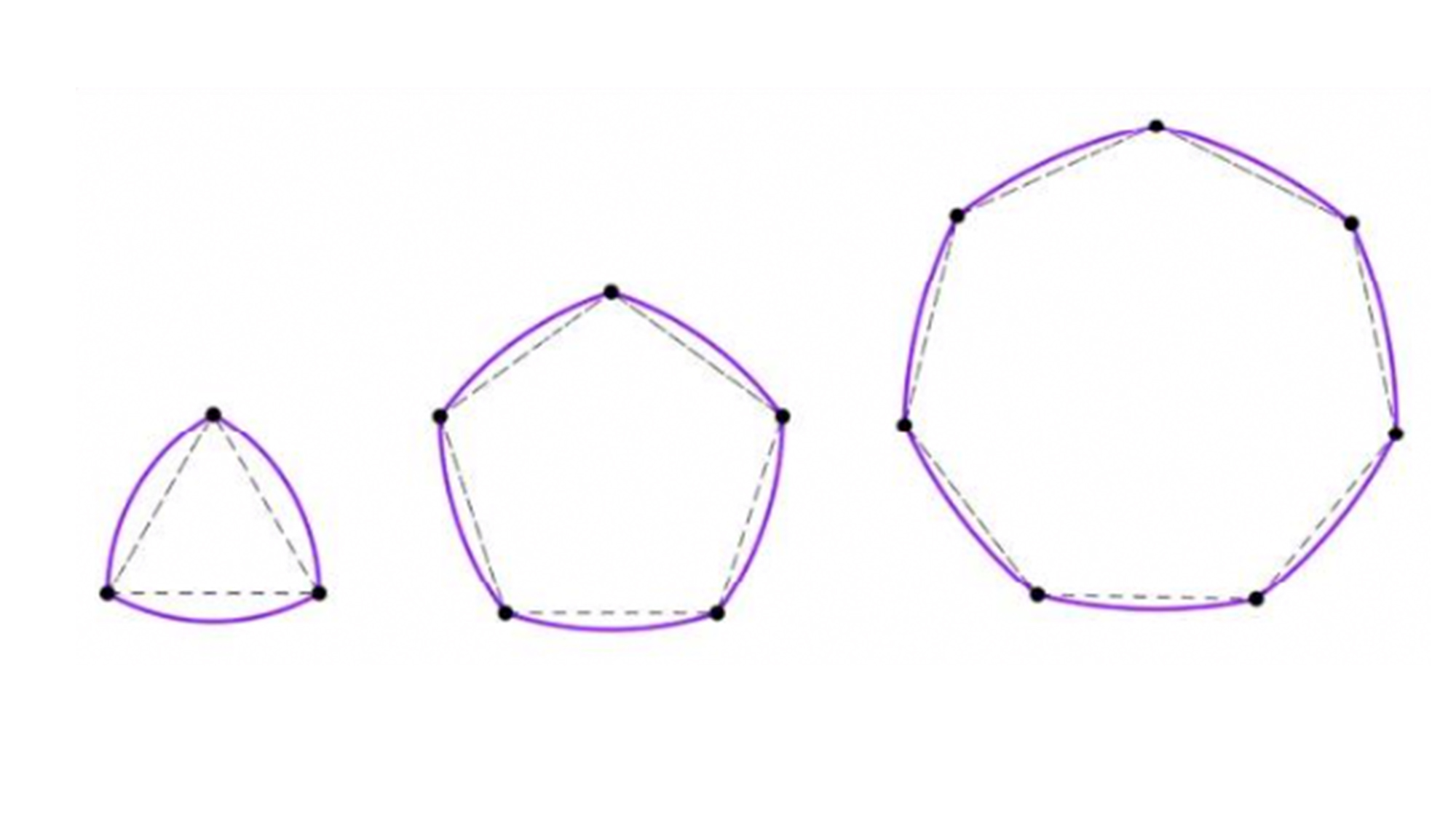
Y así, todos los polígonos de Reuleaux pueden convertirse en tapas de alcantarillado. Como estos:
Debido a sus formas, también son usadas como monedas en varios países (en Chile no), ya que son aptas para algunas máquinas expendedoras de alimentos y en juegos. En Reino Unido, por ejemplo, las usan en las de 20 y 50 peniques.
Así hay otras tantas cosas que, sin notarlo, tienen esta forma: lápices y brocas de taladros, por ejemplo. Volvamos, otra vez, al comienzo de la nota… porque, a pesar de lo fácil que es hacer un círculo, también hay tapas de alcantarilla con forma de triángulo de Reuleaux. Aquí va una foto de una, en pleno San Francisco.

De acuerdo al medio digital El País, la principal razón matemática es que la tapa no caiga por el agujero. Se trata de un tema de anchura: la distancia que hay entre dos puntos opuestos de una figura plana. Lo que en un círculo es completamente constante, puesto que la lejanía que hay entre cualquier parte del borde y su opuesto es el diámetro.
Lo anterior produce que sea prácticamente imposible que la tapa caiga por el agujero, de ninguna forma. Volvamos al comienzo de la nota. ¿Por qué no cuadradas ni rectangulares? Sencillo. Porque la anchura de estas figuras no es constante, es decir, la distancia entre dos vértices opuestos es mayor que cualquiera de los lados, por lo que existe el riesgo que las tapas, estando horizontales al suelo, caigan a la alcantarilla. No vamos a negar que existen tapas cuadradas y rectangulares, pero para esto también hay una justificación, aunque algo más simple: la profundidad de los hoyos es menor, por lo que si caen, se pueden volver a poner con facilidad.

Pero el círculo no es la única figura geométrica que tiene las propiedades necesarias para ser tapa de alcantarilla. De hecho, cualquier polígono regular con un número impar de lados puede serlo. ¿Cómo? Convirtiéndolos en polígonos de Reuleaux, creados por el ingeniero alemán Franz Reuleaux en el siglo XIX aunque, según cuenta la historia, aparecía ya en algunos escritos de Leonardo Da Vinci. Pongámonos friki: el triángulo de Reuleaux es el más fácil de construir desde la base de uno equilátero, trazando tres circunferencias cuyos centros sean los vértices de la figura. ¿Todo bien? Pues, lo que queda al medio de la imagen es lo que queríamos lograr.

Y así, todos los polígonos de Reuleaux pueden convertirse en tapas de alcantarillado. Como estos:
Debido a sus formas, también son usadas como monedas en varios países (en Chile no), ya que son aptas para algunas máquinas expendedoras de alimentos y en juegos. En Reino Unido, por ejemplo, las usan en las de 20 y 50 peniques.
Así hay otras tantas cosas que, sin notarlo, tienen esta forma: lápices y brocas de taladros, por ejemplo. Volvamos, otra vez, al comienzo de la nota… porque, a pesar de lo fácil que es hacer un círculo, también hay tapas de alcantarilla con forma de triángulo de Reuleaux. Aquí va una foto de una, en pleno San Francisco.

